데이터 양이 충분하다면 굳이 보간법을 쓸 필요가 없을듯 한데요 ^^;

시간에 따라 지속적으로 처리해줘야 한다면 보간법은 사족일듯 싶습니다.

시간 간격이 일정하다면 간단하게 빼기를 하면 미분이 되니까요 ㅋㅋ

f(n + 1) - f(n)   <= 이거면 충분할것 같은데요.

정확한 값을 원한다면 시간도 고려해야겠지만 그래프만 그린다면 간단하게 하는것이 좋겠군요

장성호 님이 쓰신 글 :
: 이건 순전히 제 생각입니다.
: 관련 일이나 전공지식도 없으니 참조만 하세요
:
:
:
: 음 들어오는 데이타는 이산이잖아요
: 그걸 직선으로 연결해도 연결되는 지점에서 각도가 팍 꺽기나까 .. 미분가능한 곡선이 안되겠죠?
:
: 즉 먼저 들어오는 데이타를 받아서 그걸 미분가능한 방정식으로 만들어야 할것 같습니다.
: 이때 보간법이라는걸 사용합니다.
:
: 보간법에는 여러가지가 있는데...
:
: 점과 점을 직선으로 연결하는것은 선형보간 ==> 근데 이건 모든x 값에 대해 미분은 불가능하구..
:
: 그밖에  라그랑제 , 뉴튼 , 스플라인 등의 보간 법이 있습니다.
: 위 보간법도 여러가지로 또 나눠지구요
: 전부다 미분가능한 것은 아닙니다
:
:
: 만약 보간법으로 방정식을 구했다면...
:
: F(x) = aX^n + bX^(n-1) ..... + val ;
:
: 기울기는 한번만 미분하면 되니까..
:
: f'(x) = a*n*X^(n-1) ....
:
:
:
: 여튼 제말은 보간법이라는걸 적용해보시면 어떨까 하는 생각입니다.
:
: 그럼
:
:
: 김정모 님이 쓰신 글 :
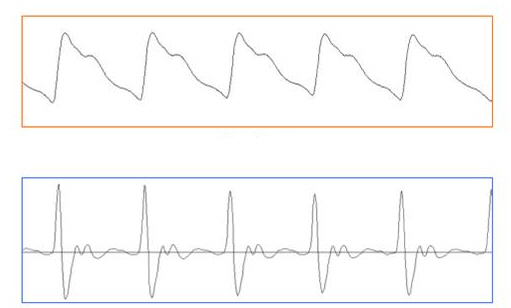
: : 첨부된 그림중 위에 그래프처럼 데이터가 날아옵니다.
: : 이걸 아래 그림처럼 미분해서 가속도 형태의 그래프로 표현하고자 합니다.
: : 수학적 지식이 부족하다보니 도움이 필요합니다.
: : 위의 그래프 데이터 형은 단순히 1차원 배열형태로 들어옵니다.
: : 그래프를 그리는 방법은 각종 챠트 컴포넌트를 이용하던지 아님 직접 그릴 예정인데
: : x축 값은 일정한 간격이지만 y축 값을 계산하는 방법이 궁금합니다.
: : 부드러운 그래프 표현을 위해서는 Laplacian of Gaussian Filter를 이용하라고 하던데
: : 구현 방법이 궁금합니다. 어떤 내용이든 관계 없습니다. 도움주시면 정말 감사하겠습니다